Cubic Surfaces
A visualization of real lines on real cubic surfaces, Sep 12, 2023
Given an object, one of the first questions you could ask is what it looks like. Unsurprisingly, understanding what such objects look like can then be used to study the objects themselves. The problem is to do this visualization carefully enough that it actually gives useful information.
The study of cubics is particularly interesting because despite being a well-studied object for hundreds of years in the field of algebraic geometry (and entire books involving calculations on such surfaces), their properties continue to inspire plenty of research.
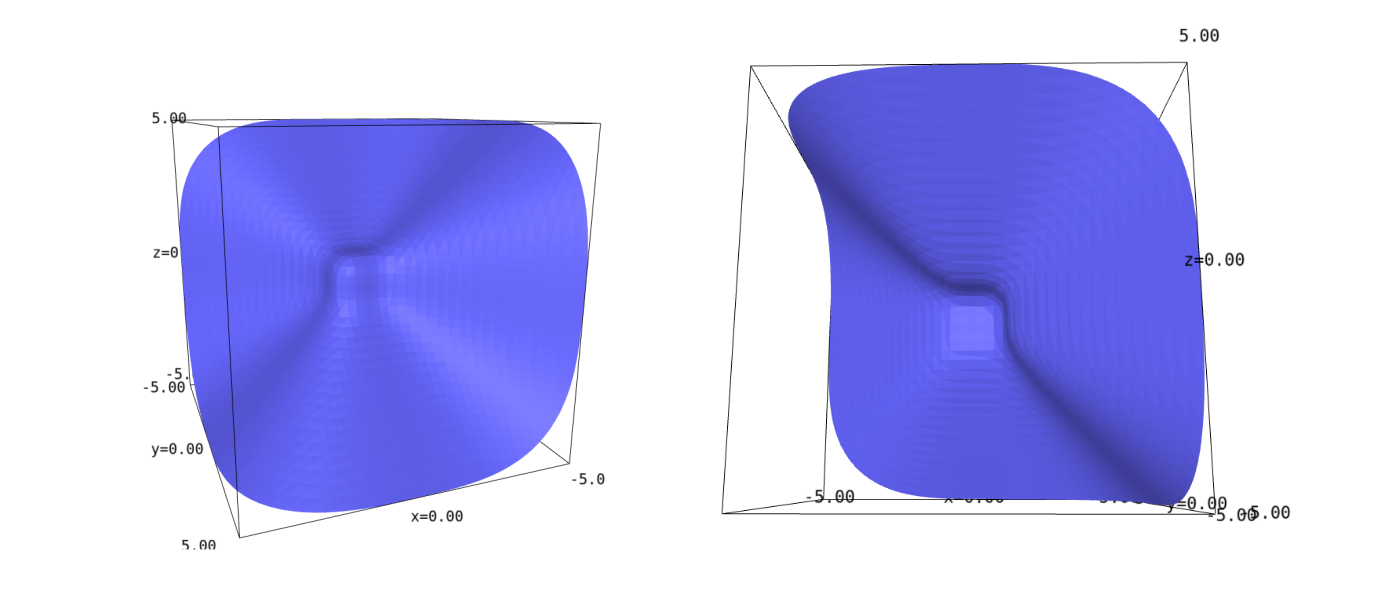
Here, a cubic refers to either a polynomial equation, such as \(f(x,y,z,t)=x^3+z^3+y^3+t^3\), or the surface containing points \((x,y,z,t)\) where \(f(x,y,z,t)=0\). Above, we have the Fermat cubic, which is defined by \(f(x,y,z,t)=x^3+y^3+z^3-t^3\). Points on the surface can either involve complex or real numbers, and surfaces over either are interesting. When you plot the objects, there are often lines sitting on the surfaces, which is strange, given the curvy nature of such surfaces. In this project, I set out to study these lines.
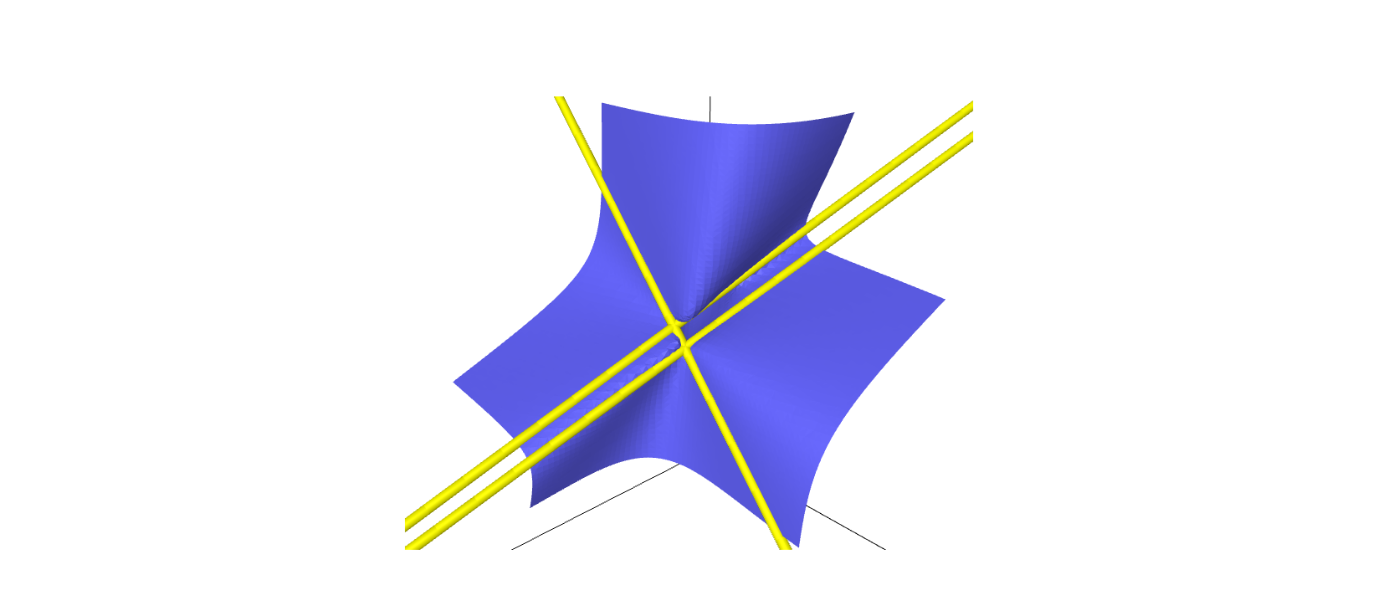
One foundational result in algebraic geometry is that there are precisely 27 lines on a cubic surface. This beautiful result from the 1800s has further inspired research on cubic surfaces even to this day, even leading to a themed list of open research questions. Not all of the lines are visible over just the real numbers. This project aims to understand cubic surfaces in terms of the lines that are visible over the real numbers. Furthermore, line behavior is only nice when the cubic surfaces are smooth. This corresponds to the surface actually looking smooth--there are no sharp cusps or nodes (see the center of the below surface for a node).
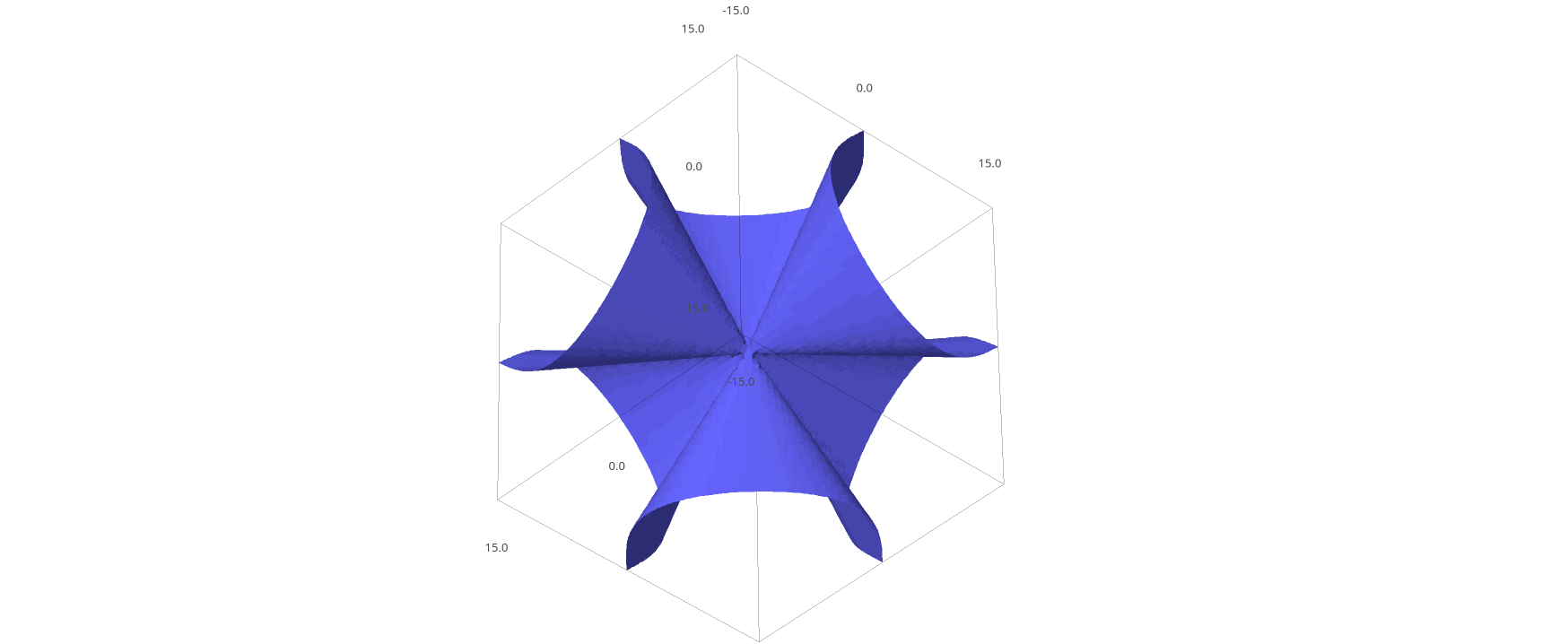
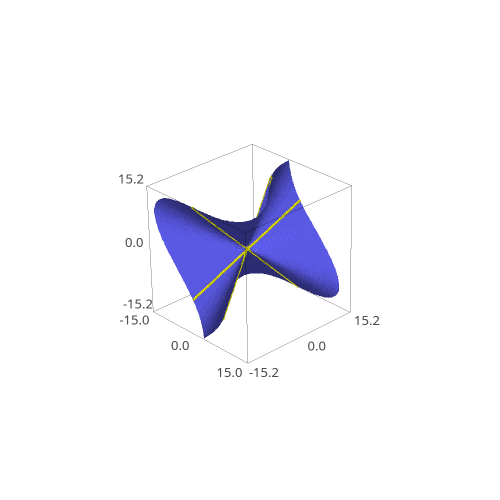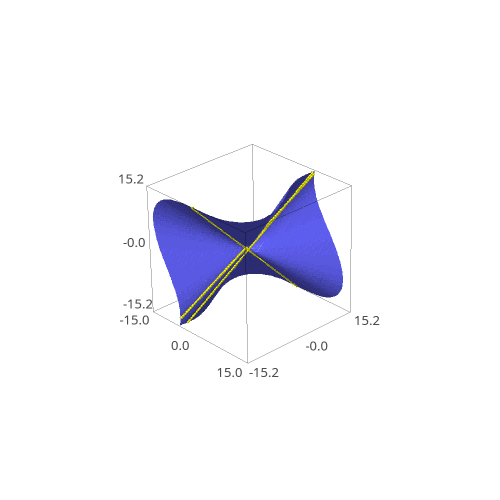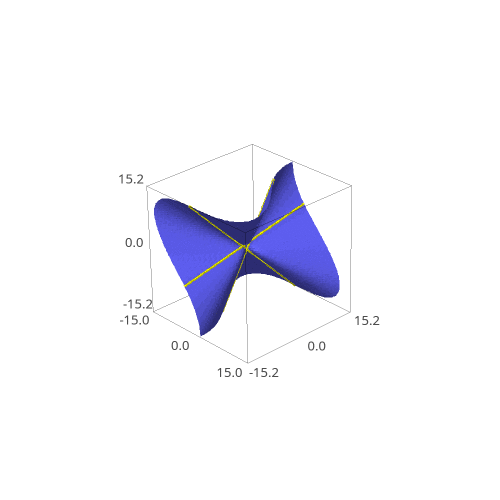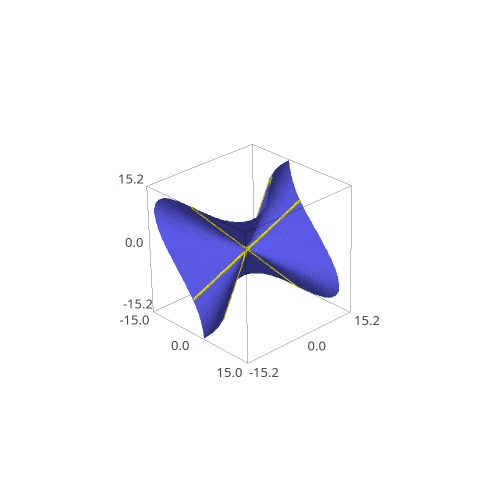
Interesting behavior is bound to happen when you change a cubic surface into another and back into itself. The lines could shuffle between each other, or even flip in orientation. Using this information, we could understand a lot on how smooth cubic surfaces behave. Consequently, I created graphing software to animate a changing cubic surface and its lines. An interesting question arises in the creation of this software.
First was a paradox in terms of what we wanted to study. We want to animate only the smooth cubic surfaces to understand such surfaces, but to do this we require an understanding of what makes a cubic surface smooth. To address this problem, there is a calculation done by George Salmon, one of the mathematicians who proved there are 27 lines, that demonstrates a rephrasing of this question. Cubic surfaces can generally be expressed in terms of cubes of five linear forms \(\ell_1,\ell_2,\ell_3,\ell_4,\ell_5\) where \[\ell_1+\ell_2+\ell_3+\ell_4+\ell_5=0\] (Here, a linear form refers to a degree 1 polynomial such as \(\ell=x+y-z\)). In particular, a cubic polynomial \(f\) can generally (according to a paper by Anna Siegal and Eunice Sukarto) be expressed as a sum \[f=\ell_1^3+\ell_2^3+\ell_3^3+\ell_4^3+\ell_5^3\] As it turns out, we know a lot more about what makes a smooth cubic surface for such cubics! To imagine a space in which cubics could change, we use not the space of coefficents \(a_0,\dots,a_{19}\) and cubics in which each \(a_i\) yields a coefficient for a cubic monomial, but where each \(a_i\) yields a coefficient for one of the linear forms \(\ell_j\). Once we do this, there is a precise description of the non-smooth cubics through a polynomial called the discriminant \(\Delta(a_0,\dots,a_{19})\). It vanishes when the corresponding cubic is non-smooth. An implementation for calculating the discriminant for the mentioned cubic surfaces is available under the github respository.
With this alternative space for visualizing cubics, we can visualize only smooth cubic surfaces changing! The visualization program is available on the repository, along with instructions on how to use it. For a sample, here's a button that plots an animation that passes through the discriminant (please be patient--cubic surfaces take a long time to bake).
Here is also a gif of the same animation in slightly lower quality.
All of the code can be accessed at this page.
This project was part of an Independent REU with the University of Utah Department of Mathematics. If you're considering it, I can't guarantee that you'll experience gnarly surfaces, but I highly recommend it!